基数変換と「有限小数」— 平成２０年度過去問の本質
目次
1. 問題
基数変換に関する記述のうち，適切なものはどれか。
| 選択肢 |
|---|
| ア：2進数の有限小数は，10進数にしても必ず有限小数になる |
| イ：8進数の有限小数は，2進数にすると有限小数にならないこともある |
| ウ：8進数の有限小数は，10進数にすると有限小数にならないこともある |
| エ：10進数の有限小数は，8進数にしても必ず有限小数になる |
2. 「有限小数」とは何か
小数には2種類がある：
| 種類 | 例 |
|---|---|
| 有限小数 | 0.5 , 0.25 , 0.125 |
| 無限小数 | 0.333… , 0.1 , 0.142857… |
この違いは 割っている数（分母） によって決まる。
3. 進数と「割れる数」の関係
ある進数で小数が終わるかどうかは、その進数の「基数」で決まる。
| 進数 | 基数 | 素因数 |
|---|---|---|
| 2進数 | 2 | 2 |
| 8進数 | 8 | 2 × 2 × 2 |
| 10進数 | 10 | 2 × 5 |
4. 有限小数になる一般ルール
分数
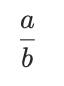
がある進数で有限小数になるのは：
分母 b の素因数が、その進数の基数の素因数だけでできているとき
つまり
| 進数 | 使える素因数 |
|---|---|
| 2進数 | 2 |
| 8進数 | 2 |
| 10進数 | 2 と 5 |
5. 各選択肢の論理チェック
ア✔ 正しい
2進数で有限
→ 分母は 2 だけでできている
→ 10進数は 2 と 5 を使える
→ 2だけならOK
→ 必ず有限小数
イ✘
8進数で有限
→ 分母は 2 だけ
→ 2進数も 2 だけの世界
→ 必ず有限
→ 「ならないこともある」は誤り
ウ✘
8進数で有限
→ 分母は 2 だけ
→ 10進数は 2 と 5 を使える
→ 2だけならOK
→ 必ず有限
エ✘
10進数で有限
→ 分母は 2 や 5 を含む
→ 8進数は 2 しか使えない
→ 5が入るとアウト
例：
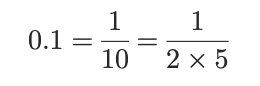
→ 10進数では有限
→ 8進数では無限小数
6. 結論
正しいのは
ア
7. 覚えるべき本質（試験対策用）
「A進数の有限小数がB進数でも必ず有限になる」 ⇔ Aの素因数 ⊆ Bの素因数
この問題は：
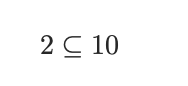
かどうかを見ているだけである。
訪問数 1 回, 今日の訪問数 1回